How to Learn Geometry Fast: 7 Proven Methods for Quick Mastery

To learn geometry quickly, start with visual learning, master core concepts such as the Pythagorean theorem and angle relationships, practice consistently with real-world problems, and consider working with an experienced tutor for personalized guidance. This combination addresses geometry’s visual and logical demands simultaneously.

Geometry challenges many students because it requires both spatial visualization and logical reasoning. Whether you’re preparing for an exam, improving grades, or seeking the best way to learn math starting with geometry, the right approach makes all the difference.

Why Learning Geometry Efficiently Matters

Geometry forms the foundation for real-world applications in architecture, engineering, computer graphics, and data visualization. High school geometry and middle school geometry courses serve as prerequisites for trigonometry, calculus, and physics.

Beyond academics, geometry appears in everyday life constantly. From calculating surface area when planning renovations to understanding parallel lines and perpendicular lines in construction, these concepts have practical applications. Students who master geometry efficiently gain confidence in problem-solving and develop critical thinking skills.

The time-sensitive nature of academic progress makes understanding how to learn geometry fast particularly valuable. College applications, standardized tests like the SAT and ACT, and GPAs all depend on geometry performance.

Understanding Essential Geometry Concepts

Before implementing accelerated learning strategies, establish a solid foundation in basic geometry terminology and principles. Knowing how to learn geometry step by step begins with mastering these fundamentals. This groundwork prevents confusion later and ensures smooth progress through complex topics.

Core Geometric Terms You Need to Know

Familiarize yourself with the fundamental vocabulary that appears throughout all geometry courses. Start with points, which represent exact locations in space, and line segments, which connect two points with a definite length.

Angles form when two rays share a common endpoint. Master the distinctions between right angles (90 degrees), complementary angles (two angles summing to 90 degrees), and congruent angles (angles with equal measures). Recognize angle relationships created when parallel lines are intersected by a transversal, producing opposite angles and corresponding angles.

Different triangles appear constantly in geometry problems, each with unique properties. Isosceles triangles have two equal sides and two congruent angles. Similar triangles maintain the same shape but different sizes, with proportional side lengths. Special right triangles include 30-60-90 and 45-45-90 triangles, which have predictable side length ratios.

The Foundation of Euclidean Geometry

Euclidean geometry provides the theoretical framework for most high school geometry courses. This system builds all geometric knowledge from five basic axioms or postulates.

The coordinate plane represents one of Euclidean geometry’s most practical applications. Mastering coordinate geometry enables you to calculate distances between points, find midpoints, and understand geometric transformations.

Working with a geometry tutor can dramatically accelerate your understanding of these foundational concepts. A skilled tutor identifies exactly which concepts you need to strengthen and creates a customized learning path.

Sources: https://accelerate.us/wp-content/uploads/2024/05/Accelerate-Research-Report-Efficiency-and-Cost-Effectiveness-1.pdf

https://www.nber.org/system/files/working_papers/w27476/w27476.pdf

7 Proven Methods to Learn Geometry Fast

Method #1: Embrace Visual Learning and Diagram Drawing

Geometry is inherently visual, making diagram construction essential for fast learning. Drawing diagrams transforms abstract concepts into concrete images that your brain can manipulate.

Develop the habit of sketching every geometry problem before attempting calculations. Use colored pencils to differentiate angles, mark equal sides, or highlight parallel lines and perpendicular lines.

Practice freehand geometric drawing to develop spatial intuition. Draw various triangles, recognizing how changing angles affects side lengths. Create your own examples of geometric transformations, including transformations rotations (turning figures around a point), translations, and reflections.

Invest in quality drawing tools that enable precise constructions. A reliable compass helps you create accurate circles. A transparent protractor allows you to measure angles without obscuring the diagram.

Method #2: Work With an Experienced Geometry Tutor

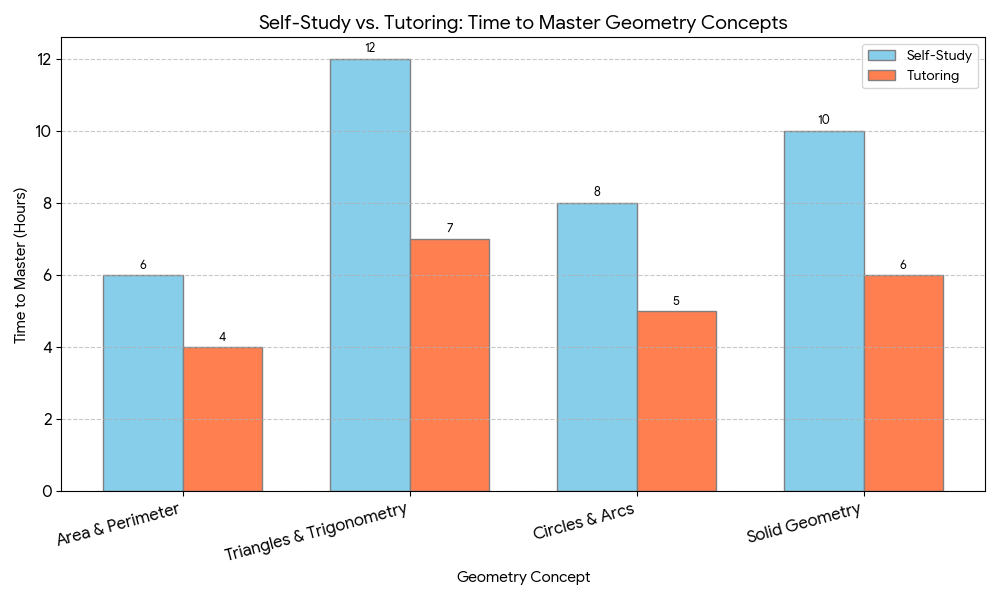
If you’re wondering how to learn geometry fast, the answer combines self-study with personalized instruction from an expert tutor. While independent practice builds skills, a tutor provides targeted guidance that eliminates confusion and prevents mistakes.

Working with a real person offers advantages that pre-recorded videos and apps cannot replicate. Tutors immediately identify misconceptions in your thinking and address them before they become ingrained habits.

The human element creates accountability and motivation that self-study often lacks. Scheduled tutoring sessions provide structure, while the relationship with your tutor makes you more invested in your progress.

LRNKEY connects students with experienced math tutors who specialize in various aspects of geometry, from basic shapes to complex proofs. The platform’s tutors set their own rates, creating competitive pricing that makes personalized instruction accessible. Many tutors offer introductory free lessons, allowing you to assess compatibility before committing.

One-on-one tutoring creates a safe environment for asking questions. Your tutor focuses exclusively on your learning goals, whether you need test preparation, homework support, or comprehensive concept mastery.

The learning process accelerates when tutors provide immediate feedback on practice problems. Rather than discovering errors later, you understand mistakes as they occur and correct your approach in real time.

Method #3: Master the Pythagorean Theorem and Core Theorems

The Pythagorean theorem represents one of geometry’s most important relationships, appearing in countless problems across various topics. This theorem states that in any right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides (a² + b² = c²).

Understanding why the Pythagorean theorem works enables you to apply it confidently in unfamiliar situations. Recognize that the theorem only applies to right triangles, preventing common misapplications.

Beyond the Pythagorean theorem, focus on understanding triangle congruence criteria (SSS, SAS, ASA, AAS). These principles allow you to prove that two triangles are identical without measuring all six parts.

The triangle inequality theorem prevents impossible triangle constructions. This principle states that the sum of any two sides must exceed the third side’s length.

Method #4: Practice Problems With Strategic Feedback

Consistent practice with geometry problems remains essential for fast skill development. However, practice quality matters more than quantity. Strategic practice focuses on problems that target your specific weak areas while gradually increasing difficulty.

Begin each practice session with warm-up problems, reviewing previously mastered concepts. Work through practice problems methodically, showing all steps even when solutions seem obvious.

Diversify your practice sources to encounter various problem-solving approaches. Textbook exercises provide structured progression, while word problems develop application skills by requiring you to translate situations into geometric models.

The most effective practice includes real-time guidance from someone who can identify exactly where your understanding breaks down. Rather than practicing mistakes repeatedly, a tutor corrects your approach immediately.

Method #5: Master Angle Relationships and Properties

Understanding how angles relate to each other forms a cornerstone of geometric reasoning. Complementary angles sum to 90 degrees, frequently appearing in right triangle problems. Supplementary angles total 180 degrees, common when working with straight lines or polygon interior angles.

When parallel lines are cut by a transversal, several angle relationships emerge. Corresponding angles are congruent, as are alternate interior angles.

Circle basics introduce unique angle relationships. An inscribed angle measures half its intercepted arc, while a central angle equals the arc it intercepts. Understanding these relationships unlocks circle geometry problems.

Method #6: Apply Geometry to Real-World Situations

Connecting geometric concepts to practical applications strengthens retention and understanding. When geometry becomes more than abstract academic exercises, your brain prioritizes the information as relevant and useful.

Look for geometry in everyday life. Calculate the surface area needed when wrapping gifts or painting rooms. Determine whether furniture will fit through doorways by considering dimensions.

Volume calculations appear constantly in practical situations. Understanding the volume of prisms helps when filling containers or estimating material quantities. Recognizing rectangular prisms in packaging design connects geometry to real products you encounter daily.

Create your own real-world geometry problems based on situations you encounter. Measuring angles in your environment or calculating areas of irregular spaces reinforces learning while demonstrating practical value.

Method #7: Study Geometric Transformations and Advanced Concepts

As you build confidence with foundational geometry, progress to the transformations unit, covering geometric transformations and complex shapes. This includes transformations rotations (turning figures), transformations translations (sliding figures without rotation), and reflections (flipping figures across a line).

Understanding how transformations affect coordinates on the coordinate plane builds spatial reasoning. Special right triangles deserve focused attention due to their frequent appearance.

Conic sections (circles, ellipses, parabolas, and hyperbolas) represent advanced topics that build on coordinate geometry. Understanding Cavalieri’s principle helps you grasp why certain volume formulas work. Calculating sector area in circles and prism volume prepares you for real-world applications.

A structured approach, whether through a geometry course or personalized tutoring, ensures proper concept progression.

Essential Tools for Learning Geometry Efficiently

Having the right tools facilitates faster geometry learning by enabling accurate constructions and measurements. A compass remains essential for drawing circles and constructing geometric figures precisely. A protractor enables accurate angle measurement, critical for verifying solutions.

Graph paper supports coordinate plane work and helps maintain proportion in freehand drawings. Digital geometry tools complement physical instruments, making geometric transformations particularly intuitive by providing visual feedback.

Developing Effective Study Strategies

Create a consistent study schedule with focused geometry sessions. Daily 30-45 minute sessions prove more effective than occasional marathon study periods. Your brain consolidates geometric concepts between sessions, making regular exposure more valuable than cramming.

Use the unit mastery approach rather than superficial coverage of many topics. This structured method shows you how to learn geometry step by step, ensuring each concept is fully understood before advancing. Combine multiple learning resources, including textbooks, online tutorials, and tutoring sessions, to reinforce concepts from different angles.

Fully understanding one geometric concept before advancing prevents weak foundations that complicate later learning. Take quiz unit tests to verify mastery before progression.

Alternate between different problem types within your study sessions. Practice theorem applications, complete construction exercises, and solve word problems in rotation.

Avoiding Common Geometry Learning Mistakes

Many students attempt to memorize geometric formulas without understanding their derivation or application context. Focus on comprehension over memorization, understanding why formulas work rather than just memorizing them.

Understanding how to learn geometry fast means avoiding these common pitfalls that slow most students down.

Neglecting to draw diagrams represents another significant mistake. Always sketch problems, even when diagrams seem unnecessary. This practice prevents mistakes and often reveals solution paths.

Perhaps the most significant mistake involves struggling alone when confused rather than seeking help. Geometry concepts build on each other, so confusion on foundational topics compounds over time. Working with an experienced tutor prevents minor misunderstandings from becoming major obstacles.

The Value of One-on-One Geometry Instruction

Research consistently demonstrates that personalized tutoring accelerates learning compared to classroom instruction alone. Personalized instruction addresses your specific knowledge gaps rather than following a predetermined curriculum.

The Socratic teaching method, where tutors guide students to discoveries through strategic questioning, develops a deeper understanding than direct instruction. This approach builds your geometric intuition and problem-solving confidence.

Immediate error correction prevents practicing mistakes that create lasting misconceptions. A tutor identifies and corrects mistakes as they occur, saving tremendous time and frustration.

Finding Quality Geometry Tutoring Resources

Look for tutors with verified credentials and positive reviews from previous students. LRNKEY’s platform includes comprehensive tutor profiles with ratings, educational backgrounds, and teaching specialties.

Consider tutors who offer introductory free lessons. These trial sessions allow you to assess teaching style compatibility before financial commitment.

Online tutoring offers advantages over in-person instruction for many students. Geographic limitations disappear, giving you access to expert tutors worldwide. LRNKEY’s marketplace model, where tutors set competitive rates, makes quality instruction accessible with starting rates around $5-7 per hour.

Frequently Asked Questions

How long does it realistically take to learn geometry?

Students typically require 4-8 weeks to grasp fundamental geometry concepts with dedicated daily practice. However, knowing how to learn geometry fast with a skilled tutor can reduce this timeline significantly.

What makes geometry different from other math subjects?

Geometry uniquely combines visual-spatial reasoning with logical proof construction. Unlike algebra’s focus on symbolic manipulation, geometry requires you to visualize relationships between shapes and articulate logical arguments.

Can I learn geometry effectively through self-study alone?

Self-study through textbooks and online resources provides valuable practice and concept introduction. However, most students significantly benefit from human guidance during the learning process. A tutor identifies misconceptions your self-study might miss and provides explanations tailored to your understanding.

Which geometry concepts should I prioritize first?

Begin with basic geometry fundamentals, including points, lines, line segments, and angles. Learning how to learn geometry step by step means mastering angle relationships, including complementary angles and congruent angles, before advancing. Develop a solid foundation with triangles, understanding different types and properties.

How important are geometric proofs for practical geometry knowledge?

While geometric proofs may seem purely academic, they develop logical reasoning skills valuable across mathematics and real-life problem-solving. Proofs teach you to construct valid arguments and identify reasoning errors.

What role does technology play in learning geometry?

Technology enhances geometry learning through interactive software, allowing shape manipulation and immediate visual feedback. However, technology supplements rather than replaces fundamental learning. Drawing physical diagrams develops spatial reasoning that passive screen interaction cannot fully replicate.

Conclusion

Knowing how to learn geometry fast requires combining proven strategies with consistent effort and expert guidance. Visual learning, regular practice with immediate feedback, mastery of core theorems, and real-world application all contribute to accelerated comprehension.

The solid foundation you build through effective geometry learning extends beyond academic benefits. Geometric reasoning develops problem-solving skills applicable throughout your life in real-world situations requiring spatial thinking and logical analysis.

Take the first step toward geometry confidence today. Explore LRNKEY’s community of experienced math tutors who can guide you through challenging concepts at your own pace. With affordable rates, flexible scheduling, and free trial lessons available, personalized geometry instruction has never been more accessible.